Entre Zénon et Hilbert, ce n’est pas fini !

Zénon, cruel Zénon !

Zénon ! Cruel Zénon ! Zénon d’Élée !
M’as-tu percé de cette flèche ailée
Qui vibre, vole, et qui ne vole pas !
Le son m’enfante et la flèche me tue !
Ah ! le soleil… Quelle ombre de tortue
Pour l’âme, Achille immobile à grands pas !

Paul Valéry, extrait de Le Cimetière marin

Qui est Zénon ?

Zénon était originaire d’Élée dans la Campanie actuelle, une région d’Italie du sud qui appartenait à la Grande Grèce. Contemporain de Socrate, il est surtout connu comme sophiste, inventeur de la dialectique qui consiste à soutenir aussi bien une thèse que son contraire(1). Derrière cet exercice de rhétorique, il est le premier à avoir eu la notion de l’infinitude du temps et de l’espace.

Zénon par ses paradoxes, a priori insensés, avait une extraordinaire intuition remise au goût du jour plus de deux millénaires plus tard comme nous allons le voir.

L’infinitude du temps

Zénon affirmait qu’Achille aux pieds légers, lors d’une course, ne pourrait jamais rattraper une tortue qui aurait 100 mètres d’avance sur lui.

En effet, à chaque fois qu’Achille tente de rattraper la tortue, celle-ci aura progressé de quelques pas. Achille devra donc à chaque fois renouveler un effort pour l’atteindre et cela à l’infini. Il ne pourra jamais combler l’espace qui le sépare de sa concurrente.

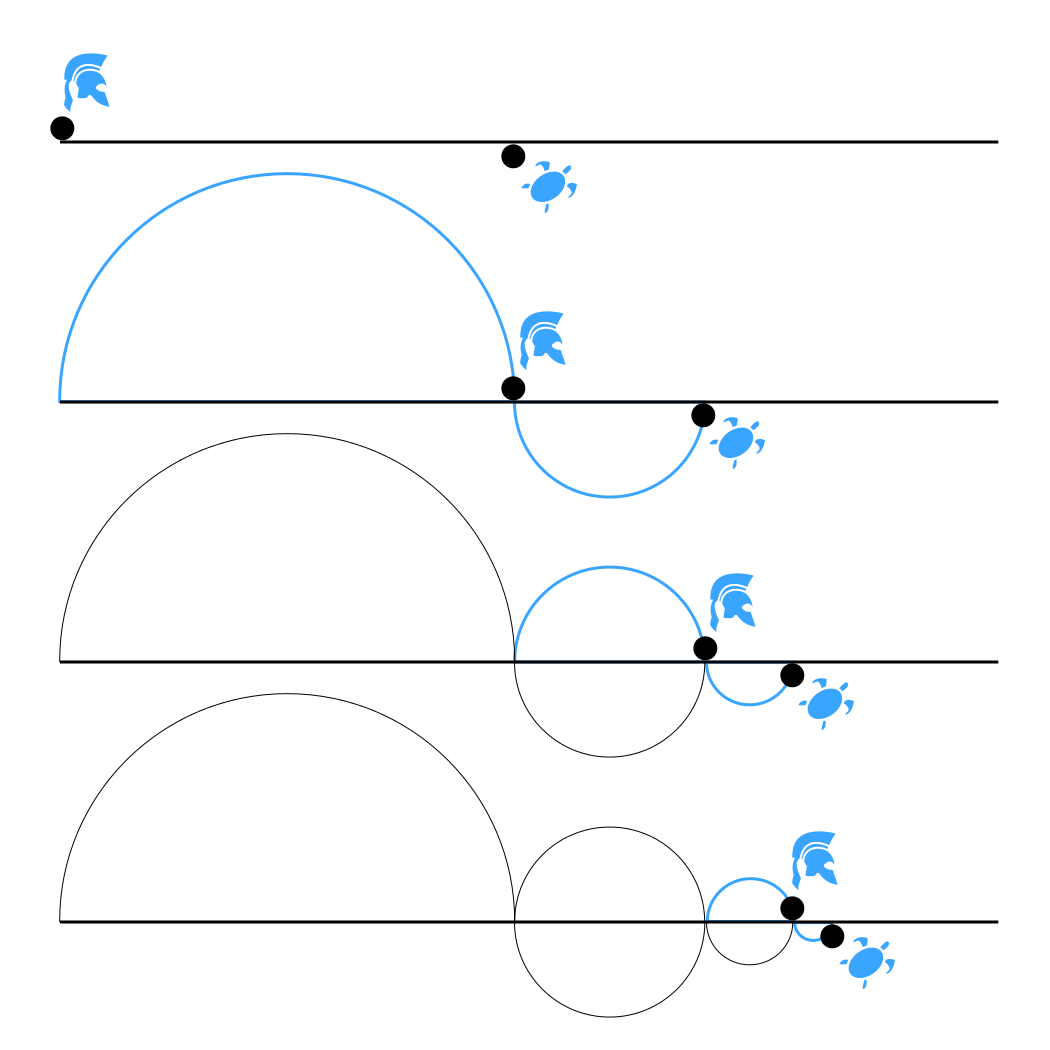
Bien sûr, la réalité contredit cette vue de l’esprit où il existe un biais : Zénon suppose qu’Achille s’arrête à chaque fois à l’endroit d’où la tortue repart.

De même Zénon soutient avec son sens de l’absurde qu’une flèche lancée par un archer, n’atteindra jamais sa cible.

Dans ce cas, la flèche à un instant donné se trouve dans une position donnée. Elle est immobile dans un espace précis. Si elle est immobile, par définition elle ne peut se déplacer. L’instant est pris comme référence absolue. Il n’y a plus de mouvement donc plus de cible à atteindre, d’où le paradoxe car bien évidemment la flèche atteindra sa cible.

Ces deux paradoxes son connus sont le nom de paradoxes de Zénon. C’est à eux que fait allusion Paul Valéry dans son poème le Cimetière marin cité en tête de cet article.

De Zénon à Heisenberg

25 siècles plus tard, ces paradoxes rattrapent Zénon.

Werner Heisenberg, prix Nobel de Physique en 1933, a défini le principe d’incertitude qui stipule qu’on ne peut pas connaître en même temps la position d’une particule quantique et sa vitesse.
Si on sait où elle se trouve, on ne peut déterminer sa vitesse et si on connaît sa vitesse on ne sait où elle se trouve.
Autrement dit, on ne peut jamais connaître sa trajectoire. Si on détermine la position de la particule, il n’y a plus de mouvement, la particule comme la flèche de Zénon se trouve immobilisée dans l’instant.

De Zénon à Hilbert ou l’infinitude de l’espace

David Hilbert (1862-1943) est un mathématicien du XXe siècle. Il redéfinit l’infini en le découpant en plusieurs infinis à la manière de la course entre Achille et la tortue. Ce paradoxe de plusieurs infinis est illustré par le fameux hôtel qui porte son nom (2).

Supposez que vous dirigiez un hôtel avec un nombre infini de chambres et que celles-ci soient toutes occupées. Une personne arrive et demande une chambre.

Que lui répondez-vous ?

— Mais, bien sûr qu’il y a une chambre. Je vais demander à tout le monde de libérer sa chambre pour prendre celle qui est à sa gauche. Vous n’aurez qu’à prendre la première.

Maintenant, une infinité de cars arrivent avec une infinité de voyageurs et tous demandent une chambre, car ils sont exténués par le voyage. Que leur répondez-vous ?

— Mais bien sûr que j’ai une chambre pour vous. Je vais demander à toutes les personnes qui occupent actuellement une chambre de prendre celle qui a un numéro double du sien.

Ainsi toutes les chambres avec un numéro impair sont libérées et les nouveaux arrivants peuvent aller tranquillement dormir.

On voit ici que, contrairement aux idées préconçues, la théorie défie parfois les évidences et réciproquement, en une sorte de poésie si bien rendue par Paul Valéry.

Article précédent : le bonheur, tout près et pourtant si loin…!